Sciencegeek Advent Calendar Extravaganza! – Day 18
by David Ng

IMAGES IN CHRISTMAS BALLS: A.K.A. CRAZY OPTICS CALCULATIONS
By Eef van Beveren, Frieder Kleefeld, George Rupp | pdf
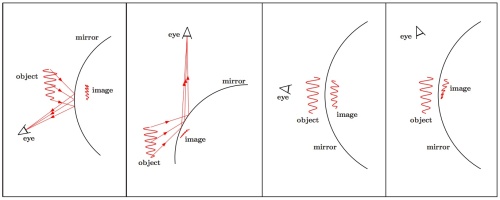
ABSTRACT: We describe light-reflection properties of spherically curved mirrors, like balls in the Christmas tree. In particular, we study the position of the image which is formed somewhere beyond the surface of a spherical mirror, when an eye observes the image of a pointlike light source. The considered problem, originally posed by Abu Ali Hasan Ibn al-Haitham — alias Alhazen — more than a millennium ago, turned out to have the now well known analytic solution of a biquadratic equation, being still of great relevance, e.g. for the aberration-free construction of telescopes. We do not attempt to perform an exhaustive survey of the rich historical and engineering literature on the subject, but develop a simple pedagogical approach to the issue, which we believe to be of continuing interest in view of its maltreating in many high-school textbooks.
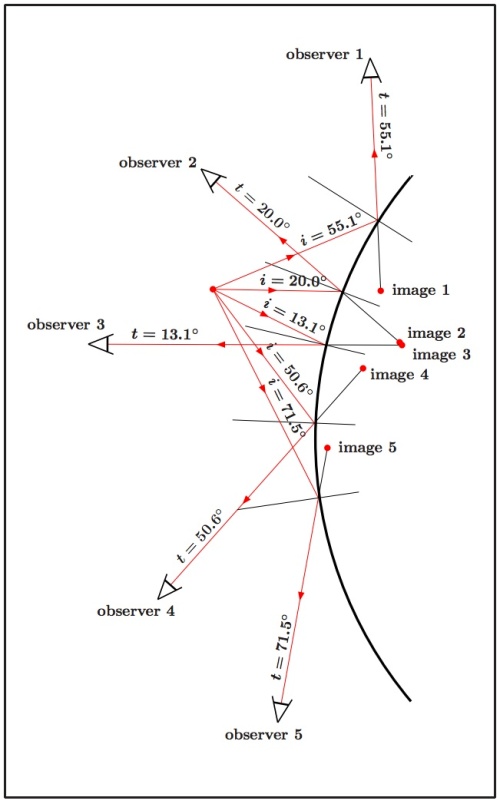
Figure 6: The locations of the various images as seen by each of the five observers introduced in Fig. 1. We also indicate the angles of incidence and reflection, in order to make sure that they are equal.
(see more of Popperfont’s Sciencegeek Advent Calendar Extravanganza here)